René Descartes
geometry
|
Cartesian coordinates
Algebra had nothing to do with geometry. Geometry had been conducted without numbers using only compass and straightedge, as Plato had taught. Numbers were for craftsmen and businessmen. But Pierre de Fermat showed that an equation could be described as a curve and René Descartes showed that a curve could be described by an equation. The work of Descartes was difficult and incomplete. Translated into Latin and explained, however, it correlated geometry and algebra and enabled the development of calculus.
Analytic geometry
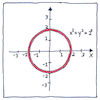
The beauty of x2 + y2 = 1 the unit circle penetrated my befuddled head. How could high school seem so easy when I was barely aware of what I was doing there? The equations for line and circle the elegance of each solution encompassed me.
Handedness
A tribe in the South American rainforest has no word for left or right. Absolute directions are all they use. Instead of reading a page from left to right, they would need to orient the top of the page to the north for example, and read from west to east. The Mayans had one name for both blue and green although they could qualify a color to describe its hue, brightness, saturation, texture, pattern, translucence, wetness, and shape. Neither the Iliad nor the Odyssey use use a word for ‘blue’. Ancient Greeks described the sky as bronze, but wouldn’t the sky for them have been a particular kind of bronze? Are our lives more complicated? More uncertain? Perturbations and chaos have always seemed to intervene when trying to fit the ideal to life’s curves.
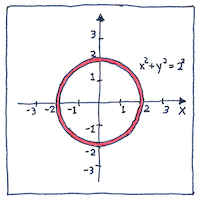


Cartesian coordinates united geometry and algebra.
Nicole Oresme and Pierre de Fermat independently invented two-dimensional and three-dimensional coordinate systems, but the publication by Descartes in 1637 had a huge influence, including facilitating the development of calculus by Newton and Leibniz. Descartes used only a single axis; commentators including Frans van Schooten added the second perpendicular axis.
See also in The book of science:
Readings in wikipedia: