Nicolai Lobachevsky, János Bolyai, Bernhard Riemann
geometry

|
Non-Euclidean geometry
On a flat world parallel lines never intersect but flat worlds don’t always intersect with the real world where some do not believe their senses accepting odd topologies in which mass increases with velocity in which gravity bends light even though we know it has no mass for gravity to pull in which the vibration of twisted and invisible dimensions are what others consider immutable in which an infinite universe never wraps around us as we fail to wrap our minds around it.
Non-Euclidean house
If all plumbs were true all paintings hung straight no door or window stuck on its jamb this house would not be be right to house this crooked man.
Postulates
It is possible to understand each other. Like foreigners forced to learn by trial and error we point to a banana and the man says “xorupeet.” We indicate two parallel lines and say “they never meet.”
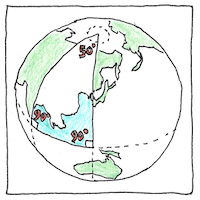


Like new math or declarative programming (compared to procedural programming), non-Euclidean geometry might be easier to conceptualize if it were your first. But any geometry is a conceptualization, not a reality. Any mathematics declares its assumptions, which it cannot prove, whereas any reality is its own proof, compared to our perception of reality, which is highly influenced by preconceptions, first teachings.
Fortunately, approximations suffice for us. Unfortunately, approximations suffice for others with conflicting views.
In Broca’s Brain, Carl Sagan says that he is often asked about UFOs and ancient astronauts, which he regards as thinly disguised religious queries, but that he would accept certain proofs, including an ancient and exotic alloy of aluminum and lead (producable only in weightless conditions), or an ancient record of “the derivation of the Lorentz transformation of special relativity”; however, without such proofs, most of us make up our minds based on incomplete evidence, generally following the procedures that we use to make other decisions in everyday life.
See also in The book of science:
Readings in wikipedia: