495 BCE

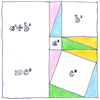
Proof of the Pythagorean theorem

• This great rule of thumb was known
• to Chinese, Indian, and Mesopotamian mathematicians,
• and helped build the great pyramids of Egypt.
• For any right triangle,
• the square of the hypotenuse is
• the sum of the squares of the other two sides.
• But Pythagoras could have been
• the first person to offer a proof of it,
• rearranging in a square four copies of the triangle.

Thales’ theorem

• A circle’s diameter
• and the chords from its end points
• to a common point on the circle
• construct a right triangle.
• Ancient trigonometry
• derived from the chord function.
• The chord of an angle between two radii
• times the radius of the circle is the distance
• between the two points on the circle.
• The chord of 60° is the radius.
• The sum of the squares
• of the chords of supplementary angles
• (whose sum is 180°)
• is the square of the diameter.

Irrational triples

• Infinitely many
• sets of three
• whole numbers
• satisfy
• the Pythagorean theorem
• and many more
• are not even rational.