Isaac Newton,
Gottfried Wilhelm Leibniz
mathematics
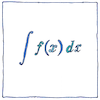
|
Calculus
Newton started with differentiation; Leibniz started with integration. Newton called it the “science of fluents and fluxions”; Leibniz called it the “calculus.” Newton was the first to apply it; Leibniz was the first to publish it. Newton focused on motion and magnitudes; Leibniz focused on the tangent and on the idea of change.
Foundations
Newton’s calculus used infinitesimals to solve the problem of planetary motion, but infinitesimals were ridiculed so Newton gave geometric proofs in Principia Mathematica. Newton understood the concept of a limit, which “can approach so closely that their difference is less than any given quantity,” and proposed limits as an alternative to infinitesimals; however, it took another hundred and fifty years for mathematicians to provide a formal and rigorous definition of calculus.
Convergence
Newton knew something about the convergence of the infinitesimally small and the infinitely large. Zeno really messed people up with his paradoxes. It took genius to say, “You can actually run to the finish line.” Zeno said that motion and change are illusions, but calculus, the mathematic of motion and change, shows us why Zeno was wrong. For his first contribution to mathematics Newton generalized the binomial theorem using infinite series. Infinitesimals are arbitrarily small; choose any small number; we can choose a number that is smaller. Infinities are arbitrarily large; choose any large number; we can choose a number that is larger. However, the sum of an infinite series isn’t necessarily infinite, but can converge to a finite number.
Steps
Except for geniuses, whom I have known, people do learn this stuff one step at a time. Everything is related to everything else, pretty much, so you can relate to it. Should we take little steps and risk boring you, or big steps and risk losing you?



The derivative of a function
f(x) = yis the slope of the tangent of the curve at the point(x,y). The tangent trigonometric function, defined as the ratio of the sine over the cosine, represents the slope of the circle at the point where the radius touches the circle. Did I get that right?See also in The book of science:
Readings in wikipedia: