Jacob Bernoulli,
Leonhard Euler
mathematics
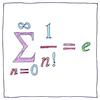
|
Euler’s number
The first irrational constant was π, known as Archimedes’ constant. The second was √2, known as Pythagoras’ constant. The third was e, known as Euler’s number. Jacob Bernoulli was the first to find Euler’s number as the result of compounding interest when the interval approaches zero, known as continuous compounding. Leonhard Euler identified e as a base for logarithms because the number 1 is common to all counting systems, because the logarithm base e of 1 is 1, and because the derivative of logarithm base e of 1 is 1.
Transcendental constant
For something characterized as transcendental, it’s odd that e pops up so frequently. as the result of continuous compounding as the probability of always losing in integral expressions for bell curves in expressions for the rate of radioactive decay in the formula for distances on a Mercator map as the area under the hyperbola 1/x between 1 and a is the natural log of a.
Approximation
Euler’s number is approximately equal to 2.718281828459045235360287471352662497757247093699959 but it is exactly equal to the limit as n approaches infinity of 1 plus 1 over n to the power of n, but go ahead and try to write that out. Without being subject to the law of diminishing returns, you may get as close as you like.
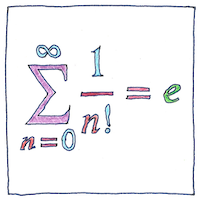


Key to the mathematical symbols:
See also in The book of science:
Readings in wikipedia:
Other readings: