Pythagoras
geometry
|
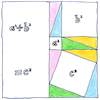
Proof of the Pythagorean theorem
This great rule of thumb was known to Chinese, Indian, and Mesopotamian mathematicians, and helped build the great pyramids of Egypt. For any right triangle, the square of the hypotenuse is the sum of the squares of the other two sides. But Pythagoras could have been the first person to offer a proof of it, rearranging in a square four copies of the triangle.
Thales’ theorem
A circle’s diameter and the chords from its end points to a common point on the circle construct a right triangle. Ancient trigonometry derived from the chord function. The chord of an angle between two radii times the radius of the circle is the distance between the two points on the circle. The chord of 60° is the radius. The sum of the squares of the chords of supplementary angles (whose sum is 180°) is the square of the diameter.
Irrational triples
Infinitely many sets of three whole numbers satisfy the Pythagorean theorem and many more are not even rational.



The X and Y axes in the Cartesian coordinate system form right angles, and the line between the origin and any point not on either X or Y axis is the hypotenuse of a right triangle. The sine and cosine in modern trigonometry are ratios of the hypotenuse with the opposite and adjacent sides of a right triangle whose hypotenuse starts at the origin of the X and Y axes and ends at the circumference of the unit circle whose center is the origin. The Greek root of the word trigonometry is trigōnon, an ancient triangular lyre or harp. The vibration of musical strings create standing waves and their form can be expressed using trigonometric functions.
Fibonacci’s method for generating Pythagorean triples seems to me to be complete. If you are interested, I can give you a Java program that implements his method.
See also in The book of science:
Readings in wikipedia:
Other readings: