Alexandre-Théophile Vandermonde,
Peter Guthrie Tait
mathematics

|
Knot theory
A cord may be wound around itself and after its two ends are fused together it will stay tied. The question arose as to how closed loops like this were to be related or distinguished. To Vandermonde, a knot was like the path of a knight in chess as it covers the board without repeating. To Lord Kelvin, an atom was a knot of aether tied to itself, which is both interesting and wrong. And this got Peter Guthrie Tait to classify all possible knots, at least up to ten crossings.
Knottiness
The minimum number of crossings is a particular knot’s knottiness—counted after undoing any nugatory crossings.
Cat’s cradle
Let me show you how to make a manger for feeding cows from a loop of string. Thread it through the fingers of your two hands and let me take the string from you.
Gordian Knot
To untangle a mess of yarn, it is not permissible to cut it. However, one reason problems remain unsolved and poems remain unwritten is a desire to obey the rules.
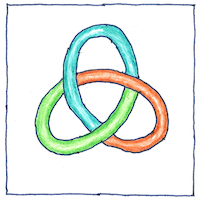


At first evolving separately, knot theory eventually became part of topology, but I must say that it seems a lot more fun working knots than solving problems in topology.
See also in The book of science:
Readings in wikipedia:
Other readings: