Felix Hausdorff,
Benoit Mandelbrot
mathematics
|
Fractal dimension
A measure of roughness A statistical index of complexity A ratio of detail to scale A measure of how completely a pattern fills a space A calculation of an object’s fractional dimension
Coastline paradox
Lewis Fry Richardson observed that the measured length of a coastline or other natural border depends on the length of the measuring stick.
Covering and packing
Construct a figure’s Hausdorff dimension by counting open balls needed to cover a figure. Construct a figure’s packing dimension by counting open balls needed to fit inside a figure. For each construction, use smaller and smaller balls.
Minkowski-Bouligand dimension
Count how many boxes of a grid are needed to cover a figure and calculate the limit as the size of the box approaches zero. A.K.A. the box-counting dimension.
More than one, less than two
How do you measure the dimension of straight line? It has a length but no width. But draw a bent line in a plane, and define the path between any two points on the line to have an infinite length. How can one say it has no width?
Self-similarity
If you have self-similarity, when we zoom in the same patterns appear. This might not be a good thing.
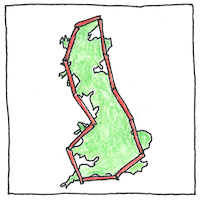


When the length of our measuring stick approaches zero, the length of the coast of Great Britain approaches infinity, which makes the length of a coastline seem indeterminable; however, the Hausdorff dimension of the coastline of Great Britain is 1.25, quite a bit more determinable.
See also in The book of science:
Readings in wikipedia: