Thales of Miletus
geometry
|
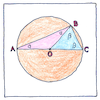
Thales’ theorem
Take the ends of the diameter of a circle, A and C, and consider any other point on the circle, B. then the triangle ABC is a right triangle. Consider the two isosceles triangles OAB and OBC. The base angles of an isosceles triangle are equal, and the three angles of a triangle add up to 180 degrees. Therefore, two α plus two β equals 180 degrees, so it is clear that α plus β equals 90 degrees, which is a right angle.
Dante’s theorem
Solomon chose wisdom so he could be an adequate king, not knowledge of the number of moving spirits in heaven, nor whether a prime mover exists, nor whether a necessary conclusion can be drawn from a necessary premise and a contingent premise, nor whether a triangle can be constructed in a semicircle that does not have a right angle.
Thales’ ideal
A point has no diameter, a line no width. A straight line has no deviation, a circle only one curvature. We do not assume these ideals; we do not pretend them. We say that any point, line, or circle drawn on wax or clay is only an approximation, only a crude representation. When our loved ones are with us, they can never be perfect. But true love is true, and can never deviate.
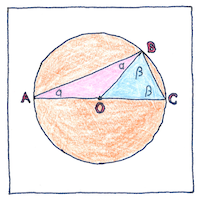


Like the Pythagorean theorem, Thales’ theorem was known by Indian and Babylonian mathematicians before Thales learned of it.
Dante’s theorem is a paraphrase of Paradiso Canto 13, lines 94-102.
See also in The book of science:
Readings in wikipedia: